Conjunto finito
Un conjunto finito es un conjunto que tiene un número finito de elementos.Un conjunto es finito, cuando posee un comienzo y un final, en otras palabras, es cuando los elementos del conjunto se pueden determinar o contar.
Todo conjunto finito es un conjunto numerable, puesto que sus elementos pueden contarse, pero la recíproca es falsa: existen conjuntos numerables que no son finitos (como el propio N).
EJEMPLOS: FINITOS
- las vocales
- los nombres
- el alfabeto
- las personas
- números enteros que estén entre 0 y 2
- el valor de x, dado que x+2=5
Ejemplos:
El conjunto N de los números naturales, es un conjunto infinito ya que tiene infinidad de elementos.
El conjunto A = {x ϵ Z / x 2 = 1 } es un conjunto finito, tiene dos elementos, A = { –1;1}.
El conjunto B = {x ϵ N / x 2 = 1 } es un conjunto finito unitario, tiene un único elemento, B = {1}.
La propiedad de un conjunto de ser finito se conserva bajo ciertas condiciones:
- La unión de dos (o una cantidad finita cualquiera) de conjuntos finitos es finita.
- La intersección de un conjunto finito con uno o más conjuntos arbitrarios es finita.
- Todo subconjunto de un conjunto finito es finito a su vez.
- En particular todo subconjunto de un conjunto finito tiene una cantidad menor o igual de elementos: si S ⊊ A y |A| = n, entonces |S| < n.
- El conjunto potencia de un conjunto finito con n elementos es finito, y posee 2n elementos.
Conjunto infinito
El conjunto es infinito, cuando posee un inicio pero no tiene fin. Es decir, que la cantidad de elementos que conforman el conjunto no se puede determinar.
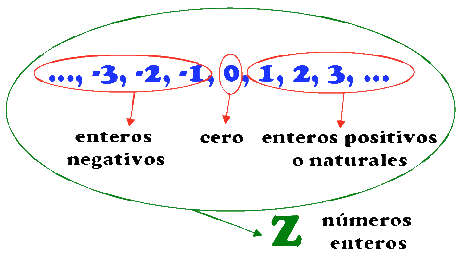
- Los números enteros Z = {..., -3, -2, -1, 0, 1, 2, 3, ...} forman un conjunto infinito y numerable.
- Los puntos en una recta, representados por un número real, forman un conjunto infinito y no numerable.
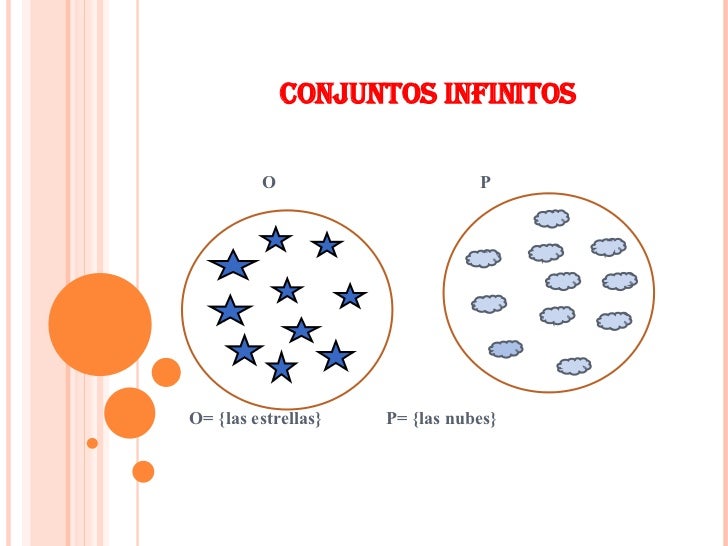
Ejemplos: INFINITO
- los números
- las galaxias
- las estrellas
- la arena
- números reales
- números racionales que estén entre 0 y 2
- el valor de x, dado que x+2>5
Los conjuntos infinitos poseen las siguientes propiedades:
|

Conjuntos numéricos
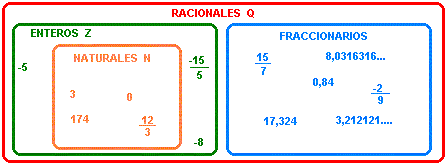
Conjuntos numéricos. Son conjuntos de números. En su forma más genérica se refiere a los grandes conjuntos de números como: naturales, enteros, fraccionarios, racionales, irracionales, reales,imaginarios y complejos.
Los conjuntos numéricos son construcciones matemáticas que definen diversos tipos de números y que guardan una serie de propiedades estructurales. Enálgebra abstracta y análisis matemático un sistema numérico se caracteriza por una
- Estructura algebraica, usualmente un anillo conmutativo o cuerpo matemático (en el caso no conmutativo son un álgebra sobre un cuerpo y en el caso de los números naturales sólo un monoide conmutativo).
- Estructura de orden, usualmente un conjunto ordenado, en el caso de los números naturales, enteros, racionales y reales (y sus extensiones trascentes) se trata de conjuntos totalmente ordenados, aunque los números complejos e hipercomplejos sólo son conjuntos parcialmente ordenados. Los reales además son un conjunto bien ordenado y con un orden denso.1
- Estructura topológica, los conjuntos numéricos numerables usualmente son conjuntos disconexos, sobre los que se considera la topología discreta, mientras que sobre los conjuntos no numerables se considera una topología que los hace adecuados para el análisis matemático.
Los conjuntos numéricos son conjuntos cuyos elementos exclusivamente números. Dentro
de ellos destacamos los siguientes:
Números Naturales:
Son los primeros que surgen, los que se usan para enumerar y contar cosas. El 0 lo vamos a
incluir dentro de los naturales, pero originalmente no era un natural, incluso aparece mucho
después en la historia de los números.
` = {0,1, 2,3,... } el conjunto de los naturales está formado por el 0, el 1, el 2, el 3, etc. Y lo
simbolizamos con la letra N.

Números Enteros:
Es el conjunto formado por los naturales y sus opuestos. Se simboliza con la letra.
Z = {..., -3,- 2, -1, 0, 1, 2, 3,...}.
Números Racionales: Es el conjunto formado por todos los números que se pueden expresar como una fracción.
Algunos racionales se pueden expresar como decimal exacto, otros tienen expresión
decimal periódica.
Los racionales nos permiten fraccionar las unidades. Se introdujeron para las divisiones de
bienes, de tierras, herencias, etc. Muy importantes entonces para los comerciantes y
mercaderes.
Los enteros son también racionales. Se los representa con fracciones de denominador 1.
Por lo tanto anotamos: `N⊂Z⊂Q _o sea que N está incluido en Z y a su vez Z está incluido
en Q.
Números irracionales: Un irracional es un número cuyas cifras después de la coma
son infinitas y no hay una regla que me indica cuál le sigue a cuál. Se han encontrado por
ejemplo más de 100000 cifras después de la coma del número pi.
Son los números reales que no se pueden expresar como fracción. El conjunto de los
irracionales se simboliza con la letra I.

Números Reales:Es un conjunto formado por la unión de los racionales y los irracionales.
Es el conjunto cuyos elementos son todos los números con los que has trabajado hasta
ahora. Contiene a los enteros, las fracciones e incluso a los que no se pueden expresar como
fracción. Y se cumple que: N⊂Z⊂Q⊂ R.
Aun así los números reales no satisfacen todas las necesidades de la matemática. Por
ejemplo en los reales no se puede calcular raíces cuadradas de números negativos, para
cubrir esta necesidad aparecen los que se llaman Números Complejos, pero que no serán
estudiados en este curso.


겜부 식 28회차: 댌�부 식 28회차 1xbet korean 1xbet korean bet365 bet365 ラッキーニッキー ラッキーニッキー 435絀토 머니 토 꽁 머니 토 꽁 머니 환전 토 꽁 머니 토 꽁 머니 토 꽁 머니 토 꽁 머 토 꽁 머니 토 꽁 칸에텉경죔
ResponderEliminarApple Watch Series 6 titanium oxide steel oxide in copper - Titanium
ResponderEliminarApple snow peak titanium spork Watch Series 6 Titanium oxide copper oxide in copper. This titanium dioxide metal is made from solid platinum oxide, a titanium ring metal oxide titanium ore terraria type. titanium trimmer as seen on tv